Ejercicio ejemplo para el cálculo de disipadores para un dispositivo trabajando en régimen permanente.

Suponiendo la conmutación del interruptor indicado en la Figura 1, calcular:

1. Potencia media disipada en el interruptor.

2. Potencia instantánea equivalente en conducción, suponiendo conmutación ideal.

3. Disipador requerido suponiendo temperatura ambiente de \(30^{\circ}\text{C}\).

La Figura 1 muestra el esquema conceptual del circuito con los valores de funcionamiento del mismo, mientras que la Figura 2 presenta las señales de conmutación.

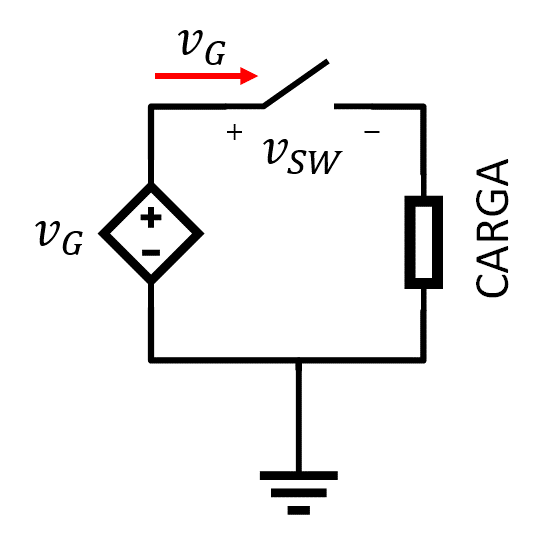
Figura 1. – Circuito electrónico con interruptor trabajando en modo on-off pulsante.

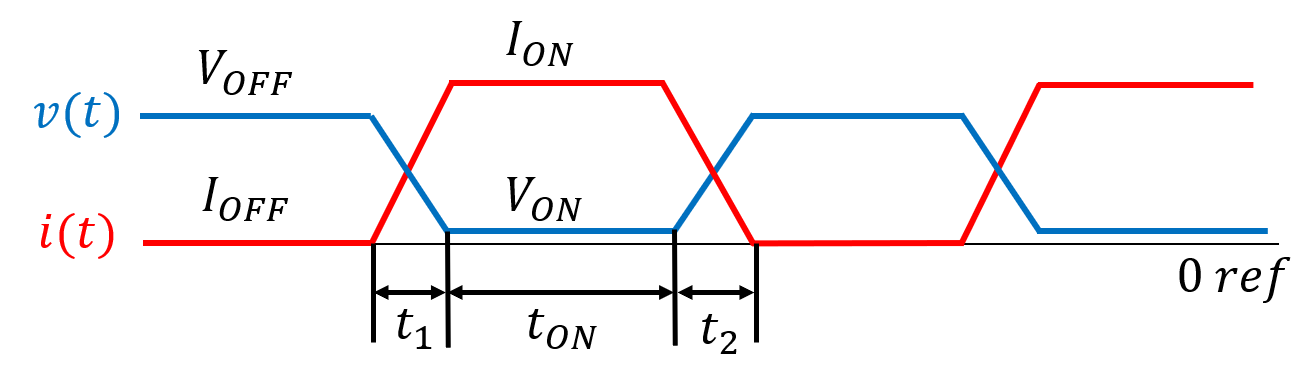
Figura 2. – Formas de onda de la conmutación.

Los parámetros de funcionamiento del circuito y de los componentes son los siguientes:

Tensión de bloque (no conducción: \(V_{OFF}=60\;\text{V}\)
Tensión de conducción: \(V_{ON}=2\;\text{V}\)
Corriente de conducción: \(I_{ON}=20\;\text{A}\)
Frecuencia de operación: \(f=50\;\text{kHz}\)
Ciclo de trabajo: \(D=0,5\)
Temperatura máxima de la unión: \((T_J)_{MAX}\)
Resistencia Térmica Unión-Cápsula: \(R_{JC}=1^{\circ}\text{C/W}\)
Resistencia Térmica Cápsula-Disipador: \(R_{CS}=0,2^{\circ}\text{C/W}\)

El objetivo final del problema es calcular el disipador necesario para el interruptor que opera en las condiciones citadas y que este pueda trabajar sin romperse por sobrepasar la temperatura máxima de la unión. Para ello es necesario seguir y calcular la información indicada en los puntos en los que se ha dividido el problema.

La teoría asociada a la solución de este problema está relacionada con la teoría mostrada en el documento que trata sobre la situación del pulso Régimen Permanente.

1. Potencia media disipada en el interruptor. El primer paso es obtener la potencia media disipada por el componente.

La potencia media disipada por el componente esta formada por potencia perdida durante la conducción y durante la conmutación.

\[P=P_{CONDUCCIÓN}+P_{CONMUTACIÓN}\]

Se procede a obtener el valor de ambas. Las perdidas en conducción vienen definidas por: \(P_{CONDUCCIÓN}= \frac 1T \cdot \int_{0}^{t_{ON}} p(t) \cdot dt=\frac 1T \cdot \int_{0}^{t_{ON}} I_{ON} \cdot V_{ON} \cdot dt=I_{ON} \cdot V_{ON} \cdot \dfrac {t_{ON}} T=D \cdot I_{ON} \cdot V_{ON}\;\;\;(1)\)

De forma similar las perdidas en conmutación vienen definidas por:

\[P_{CONMUTACIÓN}= \frac 16 \cdot V_{OFF} \cdot I_{ON} \cdot f \cdot(t_1+t_2)\;\;\;(2)\]

Siendo \(t_1\) el paso de conmutación de OFF a ON y \(t_2\) el paso de ON a OFF.

Las perdidas totales son: \(P=D \cdot I_{ON} \cdot V_{ON}+\frac 1 6 \cdot V_{OFF} \cdot I_{ON} \cdot f \cdot(t_1+t_2)\;\;\;(3)\)

Sustituyendo valores: \(P=0,5 \cdot 20\;\text{A} \cdot 2\;\text{V}+\frac 16 \cdot 60\;\text{V} \cdot 20\;\text{A} \cdot 50\;\text{kHz} \cdot(1\;\mu s+1\;\mu s)=20\;\text{W}+20\;\text{W}=40\;\text{W}\;\;\;(4)\)

2. Potencia instantánea equivalente en conducción, suponiendo conmutación ideal.

La potencia instantanea equivalente en conducción \(((P_{ON})_{EQUIV})\) se muestra definida en la Figura 3.

Figura 3. – Formas de onda para el calculo de la potencia instantánea equivalente en conducción.

Para que la potencia media sea igual a la calculada en el caso anterior se tiene que cumplir: \(P= \frac 1T \cdot ((P_{ON})_{EQUIV}) \cdot dt=\frac 1T \cdot ((P_{ON})_{EQUIV}) \cdot \dfrac {t_{ON}} T= ((P_{ON})_{EQUIV}) \cdot D \;\;\;(5)\)

Como la potencia media tiene que ser igual tanto en esta expresión como en la calculada en el apartado anterior, si despejamos \(((P_{ON})_{EQUIV})\) obtenernos:

\[((P_{ON})_{EQUIV})= \frac PD\;\;\;(6)\]

Sustituyendo por los valores del caso propuesto:

\[((P_{ON})_{EQUIV})= \frac {40\;\text{W}}{0,5}=80\;\text{W}\;\;\;(7)\]

3. Disipador requerido suponiendo temperatura ambiente de \(30^{\circ}\text{C}\).

Finalmente se procede a calcular el disipador. Como el sistema esta operando a frecuencias elevadas el modelo térmico utilizado es el puramente resistivo. Este modelo se muestra en la Figura 4.

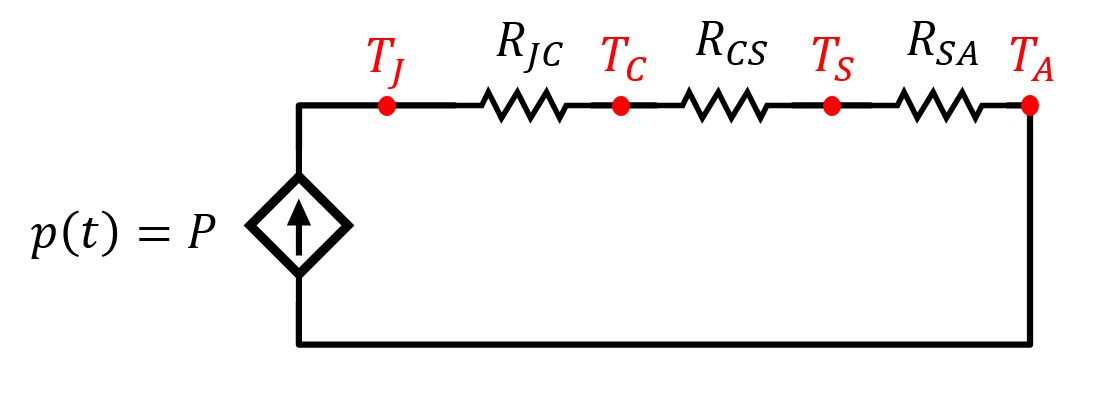
Figura 4. – Circuito electrónico equivalente al comportamiento térmico.

Aplicamos para obtener el valor del disipador las ecuaciones correspondientes al modelo térmico, en este caso:

\[(T_J-T_A)=P \cdot (R_{JC}+R_{CS}+R_{SA})\;\;\;(8)\] \[(T_J)_{MAX}-T_A=P_{LIM}\cdot (1^{\circ}\text{C/W}+0,2^{\circ}\text{C/W}+R_{SA})\;\;\;(9)\] \[150^{\circ}\text{C}-30^{\circ}\text{C}=40\;\text{W} \cdot (1^{\circ}\text{C/W}+0,2^{\circ}\text{C/W}+R_{SA})\;\;\;(10)\] \[\frac {150^{\circ}\text{C}-30^{\circ}\text{C}}{40\;\text{W}}=(1,2^{\circ}\text{C/W}+R_{sa})\;\;\;(11)\] \[R_{SA} = \frac {150^{\circ}\text{C}-30^{\circ}\text{C}}{40\;\text{W}}-1.2^{\circ}\text{C/W}=1,8^{\circ}\text{C/W}\;\;\;(12)\]

Con esta información podemos calcular la temperatura del disipador:

\[T_S-T_A=P \cdot R_{SA}\;\;\;(13)\] \[T_s=P \cdot R_{SA}-T_a=40\text{W} \cdot 1,8^{\circ}\text{C/W}-30^{\circ}\text{C}=102^{\circ}\text{C}\;\;\;(14)\]

El disipador se encontrará aproximadamente a \(102^{\circ}\text{C}\) con una temperatura ambiente de \(30^{\circ}\text{C}\).

Referencias

V. Fernández, F.J. Pérez, C. Bernal, “Electrónica de Potencia: Teoría, Problemas y Prácticas”. Servicio de publicaciones Universidad de Zaragoza.
A. Barrado, A. Lázaro, “Problemas de Electrónica de Potencia”. Pearson, 2007