Impedancia térmica transitoria (tren de pulsos)

La aproximación ideal de la onda de potencia supone incluir en el valor permanente de conducción la contribución de los transitorios de conmutación. Por tanto, se utiliza un valor equivalente de la potencia instantánea en conducción, \(P_{on}\), relacionado con la potencia media, \(P\).

\[P=\frac{1}{T} \int_0^{t_{on}}P_{on} \cdot dt =D \cdot P_{on}, \quad P_{on}=\frac{P}{D}, \quad D=\frac{t_{on}}{T}\]

Donde \(P\) es la resultante de los términos estacionario y de conmutación.

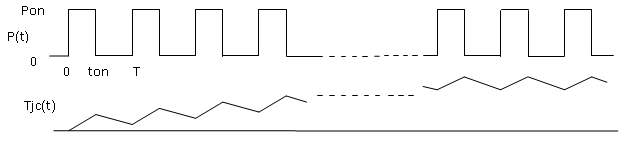
Figura 1. – Comportamiento térmico de un integrado frente a un tren de pulsos.

Con la excitación indicada, la situación puede explicarse mediante un proceso repetitivo de carga-descarga de las capacidades del circuito equivalente, en correspondencia con los intervalos de calentamiento y enfriamiento, respectivamente, de modo que el gradiente térmico unión-cápsula,\(T_{jc}\), va elevándose hasta estabilizarse en un régimen permanente de sucesivas fluctuaciones (rizado) alrededor de un valor medio, donde éste es la respuesta estacionaria a la componente continua de excitación y, por consiguiente, con los condensadores en circuito abierto. Sin embargo, ese valor medio del gradiente térmico puede ser poco relevante en el caso de que las fluctuaciones sean importantes, por lo que resulta de interés determinar el correspondiente valor máximo.

Debido al mayor valor de las capacidades, se despreciarán en régimen permanentes las variaciones térmicas de la cápsula y del posible disipador, lo que significa aproximar los condensadores asociados como cortocircuito a todos los armónicos de la onda rectangular de excitación, mientras que a la componente continua de ésta actúan, obviamente, como circuito abierto. De este modo, la cápsula y el disipador pueden suponerse a temperaturas fijas, determinadas por los valores de las correspondientes resistencias térmicas y de la potencia media, mientras que las fluctuaciones quedan restringidas a la unión.

Modelo de circuito eléctrico transitorio equivalente

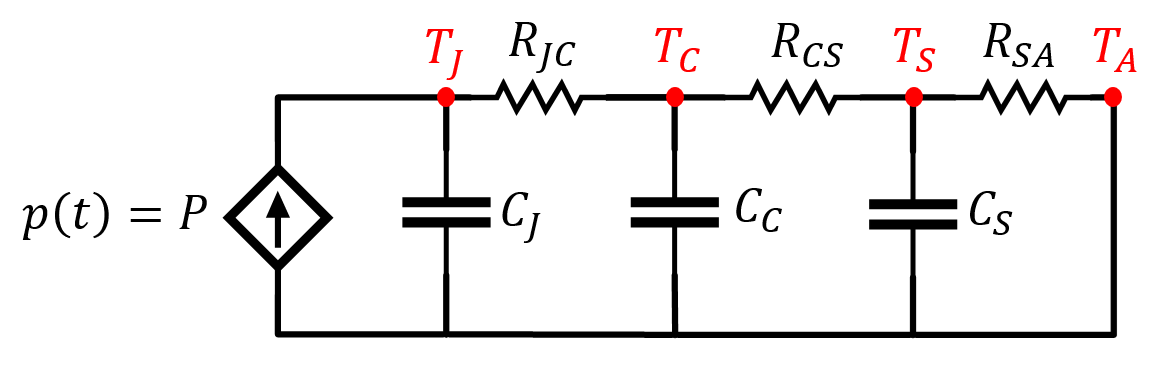
Figura 2. – Circuito eléctrico equivalente a comportamiento térmico de un dispositivo.

\[p(t)=P+\sum_{n=1}^\infty P_n w_n\] \[C_j\ll C_c\ll C_s\]

Las impedancias de los condensadores son del tipo \(\mid Z \mid=\frac{1}{C \cdot \omega}\).

Si \(C_c\) y \(C_s\) son lo suficientemente grandes como para considerar que a frecuencias bajas \(Z_c\) y \(Z_s\) tienden a \(0\), se comportan como cortocircuitos.

Dado que el problema puede dividirse en una situación continua más una variable en régimen permanente con un nivel de continua asociado y cada una puede asociarse a distintos elementos del circuito, dividimos el circuito y analizamos el problema por separado.

Componente incremental

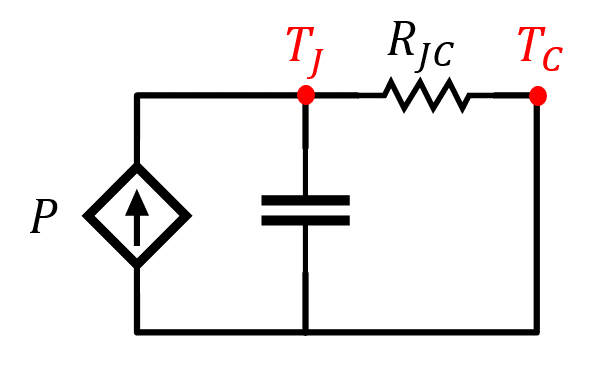
Figura 3. – Circuito eléctrico equivalente de la componente incrementar referente al comportamiento térmico de un dispositivo.

Circuito asociado a las variaciones de temperatura en la unión.

Componente asociada al nivel medio en régimen permanente

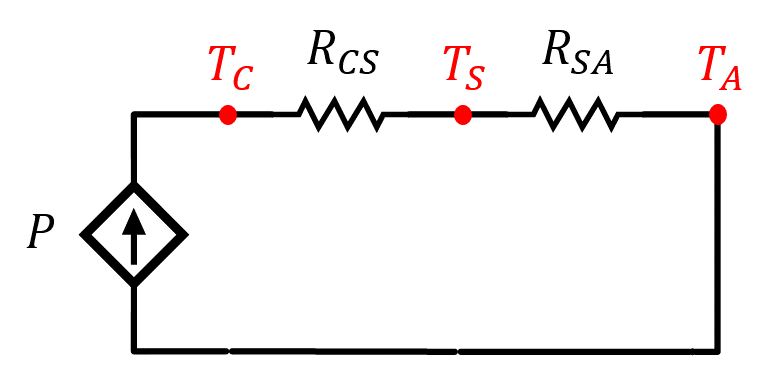
Figura 4. – Circuito eléctrico equivalente de la componente en régimen permanente del comportamiento térmico del dispositivo.

Circuito asociado a las temperaturas constantes de la cápsula y el disipador.

Analizando la situación de la unión:

• Intervalo \(t_{on}\) → Intervalo de carga de \(C_j\):

\(T_{jc}(t)=T_{jc}(\infty)+[T_{jc}(0)-T_{jc}(\infty)] e^{-t⁄\tau}\) \(T_{jc}(t)=P_{on} \cdot R_{jc}+[T_{jc}(0)-P_{on} \cdot R_{jc}] e^{-t⁄\tau}\)

• Intervalo \(t_{off}\) → Intervalo de descarga de \(C_j\):

\[T_{jc}(t)=T_{jc}(0)e^{-t⁄\tau}\]

De estas expresiones se obtiene:

\[(T_{jc})_{\max}=P_{on} \cdot R_{jc} \frac{1-e^{-t_{on}⁄\tau}}{1-e{-t⁄\tau}}=P_{on} \cdot Z_{jc}\]

Siendo \(P_{on}\) la potencia instantánea equivalente en conducción y \(Z_{jc}\) la impedancia térmica transitoria unión-cápsula en situación pulsante.

Esta impedancia depende del tiempo de conducción, \(t_{on}\) y del ciclo de trabajo \(D\) del componente, de modo que:

\[Z_{jc}=Z_{jc}(t_{on},D)=R_{jc} \frac{1-e^{-t_{on}⁄\tau}}{1-e^{-T⁄\tau}}=R_{jc} \frac{1-e^{-t_{on}⁄\tau}} {1-e^{-t⁄D\tau}} < R_{jc}\]

De acuerdo con este resultado, las curvas de impedancia térmica \(Z_{jc}(t_{on},D)\) relativas a la correspondiente resistencia \(R_{jc}\) y, por tanto, normalizadas a la unidad, se representan en la siguiente figura, tomando el ciclo de trabajo \(D\) como parámetro.

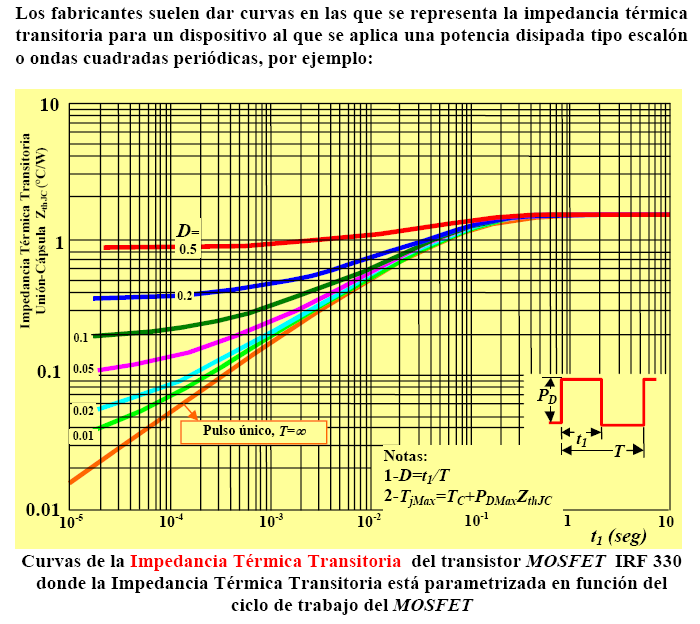
Figura 5. – Curva de la impedancia térmica transitoria.

Referencias

1. V. Fernández, F.J. Pérez, C. Bernal, “Electrónica de Potencia: Teoría, Problemas y Prácticas”. Servicio de publicaciones Universidad de Zaragoza.
2. A. Barrado, A. Lázaro, “Problemas de Electrónica de Potencia”. Pearson, 2007