Ejercicio resuelto sobre el disipador necesario en un Semiconductor trabajando como interruptor en un tren de pulsos.

Un dispositivo de potencia representado por el interruptor S mostrado en la Figura 1 se somete a un proceso de conmutación del tipo indicado en la Figura 2. Cuando el dispositivo se encuentra conduciendo suporta una tensión $V_{ON}$ y una corriente $I_{ON}$ iguales a $2\;\text{V}$ y $20\;\text{A}$, respectivamente , mientras que cuando éste se encuentra en un estado de corte soporta una tensión $V_{OFF}$ y una corriente $I_{OFF}$ iguales a $60\;\text{V}$ y $0\;\text{A}$, respectivamente. Los tiempos de conmutación del dispositivo $t_1$ y $t_2$ son igual a $1\;\mu s$; su frecuencia de conmutación, $f_S$, es $50\;\text{kHz}$ y su ciclo de operación, $D$, es $0,5$. La temperatura máxima de la unión que suporta el dispositivo $T_{Jmax}$ es $150^{\circ}\text{C}$; su constante de tiempo térmica unión-cápsula, $\tau$, es de $20\;\text{ms}$, y sus resistencias térmicas unión-cápsula, $R_{JC}$ y cápsula disiador, $R_{CD}$, son $1^{\circ}\text{C}/\text{W}$ y $0,2^{\circ}\text{C}/\text{W}$, respectivamente.

Determinar:

Potencia media total en el interruptor.
Potencia instantánea en conducción, suponiendo una conmutación ideal.
Temperatura de la cápsula y disipador requerido para una correcta operación del dispositivo, suponiendo una temperatura ambiente de $30^{\circ}\text{C}$.
Apartados anteriores para una frecuencia de operación de $50\;\text{Hz}$.

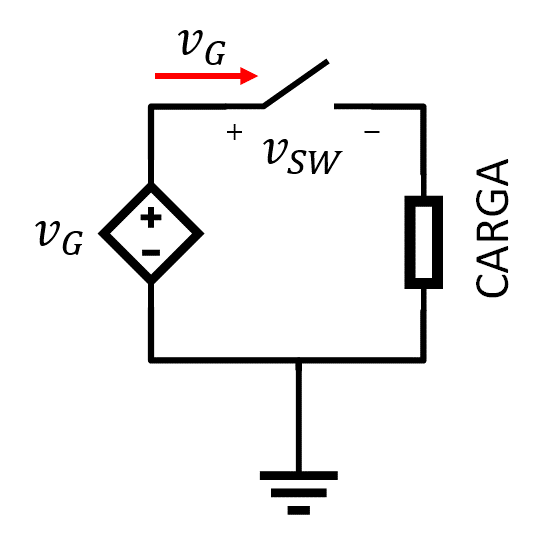
Figura 1. – Circuito de Electrónica de Potencia a analizar.

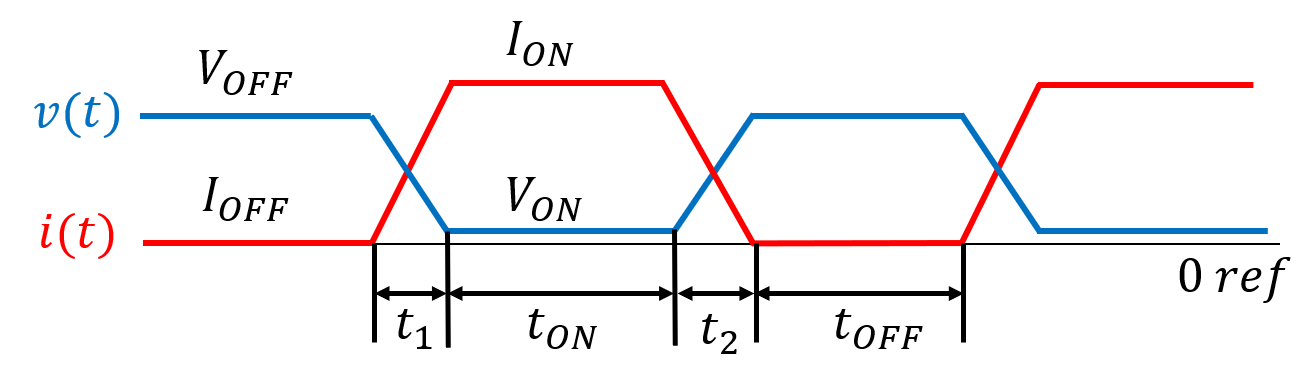
Figura 2. – Proceso de conmutación al que se encuentra sonido el dispositivo semiconductor en términos de tensión y corriente.

Solución

Apartado 1) Potencia media total en el interruptor.

La potencia media disipada por el dispositivo en conmutación, por el interruptor se puede expresar como la suma de la potencia media en conducción más la potencia media en los procesos de conmutación, como muestra la siguiente expresión: $P=P_{ON}+P_1+P_2 \;\;\;(1)$

siendo $P_{ON}$, $P_1$ y $P_2$ los valores medios correspondientes al régimen permanente en conducción y, como ya s e ha dicho anteriormente, a los dos procesos transitorios de conmutación de ${(OFF \rightarrow ON, ON \rightarrow OFF)}$.

Las potencias $P_1$ y $P_2$ disipadas por el interruptor durante los transitorios de conmutación corresponden a las siguiente expresiones:

\[P_1=\frac 1 {T_S} \cdot \int_0^{t_1} v_S \cdot i \cdot dt \approx \frac 1 {T_S} \cdot \int_0^{t_1} V_{OFF} \cdot (1- \frac t t_1 \cdot) \cdot I_{ON} \cdot \frac t t_1 \cdot dt= \frac {V_{OFF} \cdot I_{ON}} 6 \cdot \frac {t_1} {T_S} \;\;\;(2)\] \[P_2=\frac 1 {T_S} \cdot \int_0^{t_2} v_S \cdot i \cdot dt \approx \frac 1 {T_S} \cdot \int_0^{t_2} V_{OFF} \cdot \frac t t_2 \cdot (1- \frac t t_2 \cdot) \cdot I_{ON} \cdot \frac t t_2 \cdot dt= \frac {V_{OFF} \cdot I_{ON}} 6 \cdot \frac {t_2} {T_S} \;\;\;(3)\]

De la misma manera, la expresión de la potencia disipada por el interruptor en régimen permanante de conducción, $P_{CON}$, es la siguiente:

\[P_{CON} = \frac 1 {T_S} \cdot \int_0^{t_{ON}} V_{ON} \cdot I_{ON} \cdot dt = D \cdot V_{ON} \cdot I_{ON} \;\;\;(4)\]

Sustituyendo las ecuaciones anteriores 2,3 y 4 en la expresión uno se obtiene: $P=D \cdot V_{ON} \cdot I_{ON} + \frac {V_{OFF} \cdot I_{ON}} 6 \cdot f_S \cdot (t_1+t_2) \;\;\;(5)$

Finalmente sustityendo los valores proporcionados en el enunciado se obtiene: $P=D \cdot V_{ON} \cdot I_{ON} + \frac {V_{OFF} \cdot I_{ON}} 6 \cdot f_S \cdot (t_1+t_2) = 0,5 \cdot 2\;\text{V} \cdot 20\;\text{A} + \frac {60\;\text{V} \cdot 20\;\text{A}} 6 \cdot 50\text{kHz} \cdot 2 {\mu}s = 20\;\text{W} + 20\;\text{W} = 40\;\text{W} \;\;\; (6)$

Es importante destacar y hacer hincapié en la importancia que presentan la potencia asociada en los dispositivos semiconductores que trabajan como interruptores durante los procesos de conmutación. Podemos ver en este ejemplo que el valor de la potencia disipada en el semiconductor en las conmutaciones es la misma que durante el proceso de conducción.

Apartado 2) Potencia instantánea en conducción, suponiendo una conmutación ideal.

En el caso de estudio que se corresponde con un tren de pulsos repetitivo, la aproximación ideal de la onda de potencia supone incluir en el valor de régimen permanente de conducción la contribución de los transistores de conmutación, es decir, llevar la onda de estudio a una onda cuadrada de potencia ideal. A este valor de potencia en conducción lo llamaremos potencia instantánea equivalente en conducción $P_{ON}$ lo cual se relaciona con la potencia media a través del ciclo de operación D de la siguiente forma:

\[P=\frac 1 {T_S} \cdot \int_0^{t_{ON}} P_{ON} \cdot dt= D \cdot P_{ON} \;\;\;(7)\]

Donde $P$ es la potencia resultante de los términos estacionarios y de conmutación, es decir, el valor obtenido en el apartado anterior.

Por tanto, la situación presentada en el apartado anterior resulta equivalente a otra ideal, donde la potencia disipada en conmutación es nula la potencia disipada durante el intervalo de conducción coincide con $P_{ON}$.

La potencia en conducción equivalente para una conmutación ideal en el caso que nos ocupa será: $P_{ON}= \frac D P = \frac {40\;\text{W}} {0,5} = 80\;\text{W} \;\;\;(8)$

La forma de onda correspondiente a la conmutación ideal en términos de potencia se representa en la Figura 3.

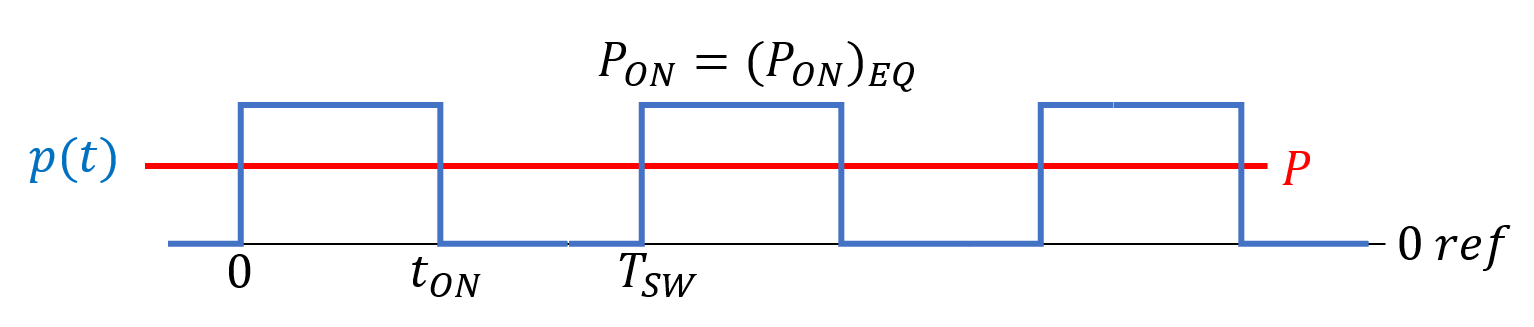
Figura 3. – Forma de onda de potencia ideal equivalente de potencia.

Apartado 3) Temperatura de la cápsula y disipador requerido para una correcta operación del dispositivo, suponiendo una temperatura ambiente de $30^{\circ}\text{C}$.

Para la resolver este apartado es necesario comprender el modelo térmico eléctrico equivalente del conjunto dispositivo-disipador mostrado en la Figura 4.

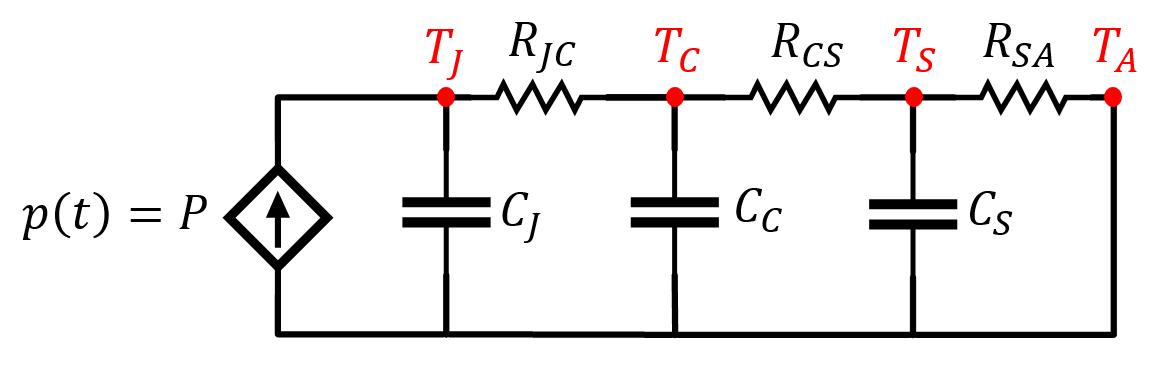
Figura 4. – Circuito eléctrico equivalente a comportamiento térmico de un dispositivo.

La teoría asociada se encuentra en el documento sobre Tren de Pulsos.

Como en dicho documento se indica, en el caso de un tren de pulsos repetitivo el comportamiento del circuito de la Figura 4, puede explicarse mediante un proceso repetitivo de Carga-Descarga de las capacidades del circuito equivalente. Esto es debido a que los condensadores se encuentran representando la inercia térmica propia de los elementos del sistema al incremento de temperaturas, y puesto que, esta inercia aumenta con la superficie de las zonas que soportan la progresión del calor, la capacidad asociada al nodo de la unión será la de menor valor del circuito.

Dicho proceso de Carga-Descarga de las capacidades del circuito equivalente se corresponde con los intervalos de calentamiento y enfriamiento, respectivamente de modo que el gradiente térmico Unión-Capsula, $T_{JC}$, va incrementándose hasta estabilizarse en un valor de régimen permanente con sucesivas fluctuaciones en torno a un valor medio, como se puede ver en la Figura 5.

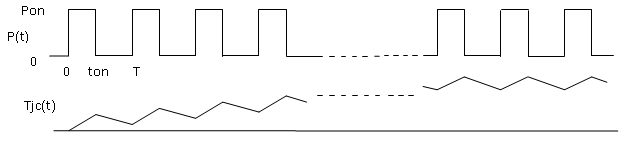
Figura 5. – Comportamiento térmico de un integrado frente a un tren de pulsos.

El valor medio del gradiente térmico puede ser poco relevante si las fluctuaciones térmicas son importantes, por eso resulta de especial interés determinar el valor máximo correspondiente.

Las capacidades térmicas de la cápsula y del disipador son mucho mayores por lo que sus variaciones térmicas se pueden despreciar, lo que permite aproximar los condensadores asociados a cortocircuitos para todos los armónicos de la onda de excitación, mientras que actúa como un circuito abierto ante una excitación continua. De esta manera, se puede suponer que la cápsula y el disipador tienen una temperatura fija, mientras que las fluctuaciones quedan restringidas a la zona de la unión. Como consecuencia directa el sistema se puede representar mediante sendos circuitos equivalentes, representados en las Figuras 6 y 7, respectivamente, siendo $p(t)$ la onda rectangular de potencia y $P$ su valor medio.

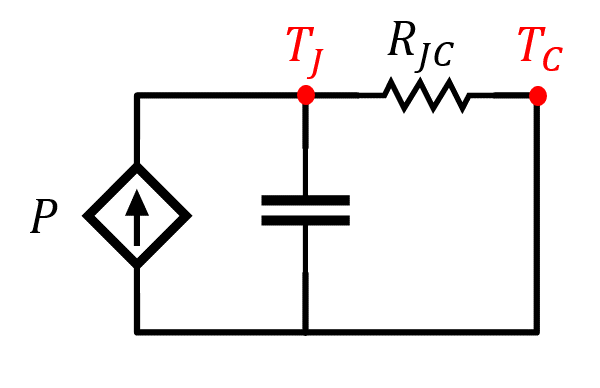
Figura 6. – Circuito eléctrico equivalente de la componente incrementar referente al comportamiento térmico de un dispositivo.

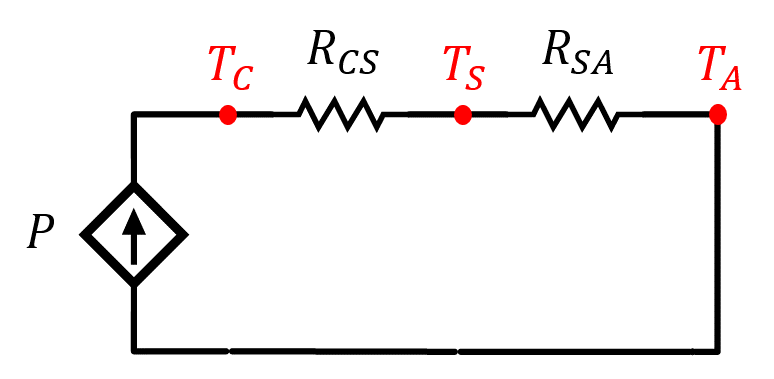
Figura 7. – Circuito eléctrico equivalente de la componente en régimen permanente del comportamiento térmico del dispositivo.

El valor máximo del gradiente térmico de la unión-cápsula en régimen permanente, definido como $({T_{JC}})_{MAX}$, viene determinado por la siguiente expresión: $({T_{JC}})_{MAX} = P_{ON} \cdot R_{JC} \cdot \frac{1-e^{-t_{ON}⁄\tau}}{1-e^{-T⁄\tau}}=P_{ON} \cdot Z_{JC} \;\;\;(9)$

Siendo $Z_{JC}$ la impedancia térmica transitoria unión cápsula en situación pulsante, $\tau$ la constante de tiempo térmica del circuito y $P_{ON}$ la potencia instantánea equivalente en conducción.

Dado que la impedancia térmica depende del tiempo de conducción, $t_{ON}$, y del ciclo de trabajo, $D$, la expresión queda definida del siguiente modo:

\[Z_{JC}=Z_{JC}(t_{ON},D)=R_{JC} \cdot \frac{1-e^{-t_{ON}⁄\tau}}{1-e^{-T⁄\tau}}=R_{JC}\cdot \frac{1-e^{-t_{ON}⁄\tau}} {1-e^{-t⁄D\tau}}\;\;\;(10)\]

Partiendo de este resultado se muestran las curvas relativas a la impedancia térmica $Z_{JC}(t_{ON},D)=R_{JC}$ relativas a la resistencia térmica $R_{JC}$ normalizadas a la unidad se representan en la Figura 8 tomando como parámetro el ciclo de trabajo.

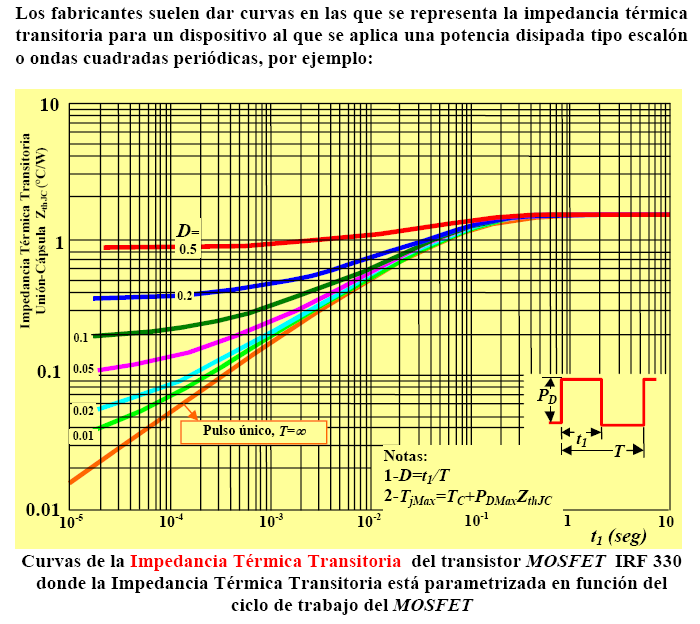
Figura 8. – Impedancia térmica transitoria unión-cápsula del pulso y ciclo de trabajo.

Cuando la frecuencia de operación es elevada $T<<\tau$ se obtiene:

\[T=(1 / f_s)<< \tau:\;Z_{JC}=R_{JC} \cdot \frac{1-e^{-t_{ON}⁄\tau}}{1-e^{-T⁄\tau}} \approx R_{JC}\cdot \frac{1-{[1-{t_{ON}}⁄\tau}]} {1-{[1-T /\tau}]} = R_{JC}\cdot \frac {t_{ON}} T = D \cdot R_{JC}\;\;\;(11)\]

El gradiente térmico máximo unión-cápsula para frecuencias elevadas viene determinado por la expresión: $(T_{JC})_{MAX}=(T_J)_{MAX}-T_C=P_{ON} \cdot Z_{JC}= P \cdot R_{JC}\;\;\;(12)$

En la situación de frecuencia elevada, el valor máximo del gradiente térmico unión-cápsula coincide prácticamente con su valor medio. Esto implica que que las variaciones de la temperatura de la unión resultan despreciables. Esto se deba a que a frecuencias elevadas todos los condensadores, incluido el asociado a la unión-cápsula se comportan como un cortocircuito a todas las componentes armónicas.

En estas condiciones el circuito térmico equivalente se puede aproximar al mostrado en la Figura 9.

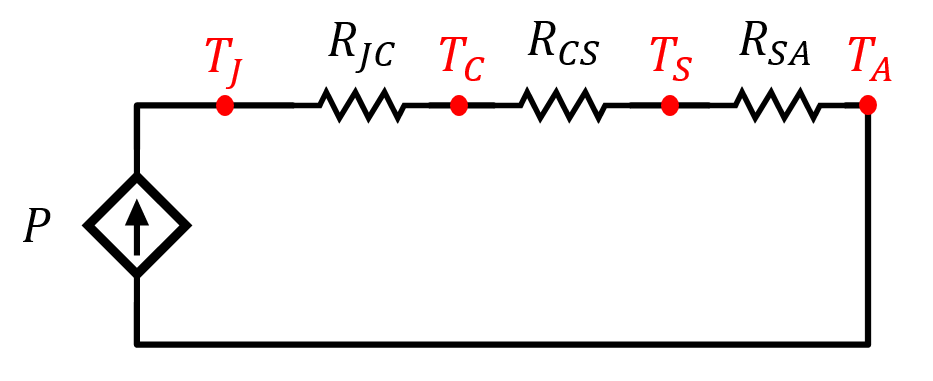
Figura 9. – Circuito térmico equivalente en continua o para frecuencias elevadas.

En este circuito las temperaturas permanecen constantes y la potencia es igual a la potencia media del circuito.

El modelo térmico de alta frecuencia, de frecuencias elevadas se corresponde con el que se obtiene cuando un circuito opera ante un régimen de excitación continua, donde para cada valor de temperatura de la cápsula, $T_C$, existe un límite de potencia, $P_{LIM}$, que se corresponde con la máxima temperatura de operación del dispositivo, es decir, la temperatura de la unión del semiconductor,$(T_J)_{MAX}$.

Esta potencia límite, $P_{LIM}$, viene definida por la expresión: $P_{LIM}(T_C)=\frac 1 {R_{JC}} \cdot [(T_J)_{MAX}-T_C]\;\;\;(13)$

Partiendo de la expresión que acabamos de definir en $(13)$ se puede determinar la temperatura de la cápsula en las condiciones dadas por el problema: $T_C=(T_J)_{MAX}-P_{LIM} \cdot R_{JC} = 150^{\circ}\text{C}-40\;\text{W} \cdot 1^{\circ}\text{C}/\text{W}=110^{\circ}\text{C}\;\;\;(14)$

Una vez obtenida esta temperatura, basta con analizar el circuito de la Figura 9. De este análisis se obtiene: $R_{SA} = \frac {[T_C - T_A - P_{LIM} \cdot R_{CS}]} {P_{LIM}}= \frac {110^{\circ}\text{C}-30^{\circ}\text{C}-40\;\text{W} \cdot 0.2^{\circ}\text{C}/\text{W}} {40\;\text{W}}=1,8^{\circ}\text{C}/\text{W} \;\;\;(15)$

Un disipador con una resistencia térmica $R_{SA}$ igual al valor calculado llevará a la unión del componente a la temperatura máxima de la unión $(T_J)_{MAX}$. Si la resistencia es mayor, la temperatura de la unión también será superior. Para garantizar que el componente se encuentra con una temperatura en la unión inferior a su valor límite la resistencia térmica del disipador deberá ser inferior al valor calculado, $1,8^{\circ}\text{C}/\text{W}$.

Apartado 4) Apartados anteriores para una frecuandia de operación de $50\;\text{Hz}$.

En estas condiciones la potencia media disipada por el componente se calcula mediante la expresión:

\[P=D \cdot V_{ON} \cdot I_{ON} + \frac {V_{OFF} \cdot I_{ON}} 6 \cdot f_S \cdot (t_1+t_2) = 0,5 \cdot 2\;\text{V} \cdot 20\;\text{A} + \frac {60\;\text{V} \cdot 20\;\text{A}} 6 \cdot 50\text{Hz} \cdot 2 {\mu}s = 20\;\text{W} + 0,02\;\text{W} \approx 20\;\text{W} \;\;\; (16)\]

Calculada la potencia podemos concluir que la potencia debida al proceso de conmutación es despreciable frente a las perdidas debidas al proceso de conmutación en régimen permanente del dispositivo.

La potencia instantánea equivalente en conducción en este caso será: $P_{ON}= \frac D P = \frac {20\;\text{W}} {0,5} = 40\;\text{W} \;\;\;(17)$

Por otro lado, también debido a la baja frecuencia de operación el interruptor las fluctuaciones en la temperatura de la unión pueden resultar significativas. Como consecuencia de ello para calcular el gradiente térmico unión-cápsula en régimen permanente es preciso utilizar la impedancia $Z_{JC}$. El valor de esta impedancia térmica se obtiene mediante la siguiente expresión, ya mostrada anteriormente.

\[Z_{JC}=R_{JC} \cdot \frac{1-e^{-t_{ON}⁄\tau}}{1-e^{-T⁄\tau}} \approx R_{JC}\cdot \frac{1-{[1-{t_{ON}}⁄\tau}]} {1-{[1-T /\tau}]} =1^{\circ}\text{C}/\text{W} \cdot \frac{1-e^{-0,01\;⁄\;0,02}}{1-e^{-0,01/ (0,5 \; \cdot \; 0,02)}} \approx 0,62^{\circ}\text{C}/\text{W} \;\;\;(18)\]

Este valor de impedancia térmica transitoria ha sido obtenido de forma analítica, si bien podría haberse obtenido de forma gráfica utilizando la gráfica mostrada en la Figura 8.

Con esta impedancia térmica se procede a obtener la temperatura de la cápsula, $T_C$: $T_C=(T_J)_{MAX}-P_{LIM} \cdot Z_{JC} = 150^{\circ}\text{C}-40\;\text{W} \cdot 0,62^{\circ}\text{C}/\text{W} \approx 125^{\circ}\text{C}\;\;\;(19)$

En estas condiciones de operación el valor de la resistencia térmica disipador-ambiente, $R_{SA}$, se calcula a partir del análisis del circuito mostrado en la Figura 7. La expresión obtenida a partir del análisis es la siguiente: $R_{SA} = \frac {[T_C - T_A ]} {P} -R_{CS}= \frac {125^{\circ}\text{C}-30^{\circ}\text{C} } {20\;\text{W}}-0,2^{\circ}\text{C}/\text{W} \approx 4,6^{\circ}\text{C}/\text{W} \;\;\;(20)$

Referencias

V. Fernández, F.J. Pérez, C. Bernal, “Electrónica de Potencia: Teoría, Problemas y Prácticas”. Servicio de publicaciones Universidad de Zaragoza.
A. Barrado, A. Lázaro, “Problemas de Electrónica de Potencia”. Pearson, 2007

Calculador de Disipadores